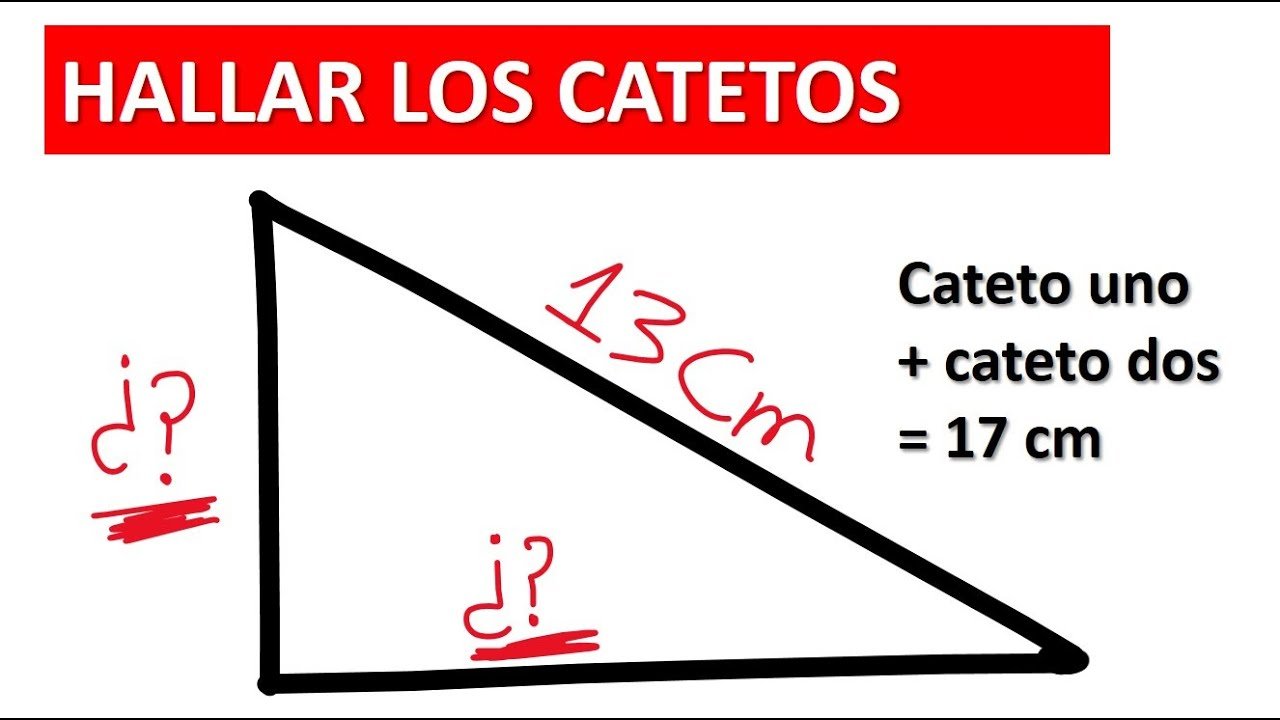
Cómo resolver triángulos rectángulos utilizando catetos y hipotenusa
Usá el Teorema de Pitágoras: a² + b² = c². Calculá un cateto con c² – cateto² = otro cateto², o la hipotenusa con a² + b² = c². Sencillo y preciso. ✅
Para resolver triángulos rectángulos utilizando los catetos y la hipotenusa, es fundamental aplicar el teorema de Pitágoras. Este teorema establece que en un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las longitudes de los catetos. En términos matemáticos, se expresa como c² = a² + b², donde c representa la hipotenusa y a y b son los catetos.
Para resolver un triángulo rectángulo, primero debes identificar las longitudes de los catetos y la hipotenusa. Si conoces las longitudes de los catetos, puedes calcular la hipotenusa. Por ejemplo, si a mide 3 unidades y b mide 4 unidades, la hipotenusa c se calcularía de la siguiente manera:
Ejemplo de cálculo de la hipotenusa
Usando el teorema de Pitágoras:
- c² = a² + b²
- c² = 3² + 4²
- c² = 9 + 16
- c² = 25
- c = √25
- c = 5
Por lo tanto, en este ejemplo, la hipotenusa mide 5 unidades.
Calculando los ángulos del triángulo rectángulo
Además de calcular la hipotenusa, también es posible determinar los ángulos del triángulo rectángulo utilizando funciones trigonométricas. Los ángulos se pueden calcular mediante:
- seno: sen(A) = cateto opuesto/hipotenusa
- coseno: cos(A) = cateto adyacente/hipotenusa
- tangente: tan(A) = cateto opuesto/cateto adyacente
Si deseas encontrar el ángulo A, puedes utilizar la función inversa del seno (arcsin) o cualquier calculadora científica. Por ejemplo, si el cateto opuesto mide 3 y la hipotenusa 5:
Ejemplo de cálculo del ángulo A
Utilizando el seno:
- sen(A) = 3/5
- A = arcsin(3/5)
Esto te dará el valor del ángulo A en radianes o grados, dependiendo de la configuración de la calculadora.
Al aplicar estas fórmulas y conceptos, podrás resolver cualquier triángulo rectángulo, determinando tanto la longitud de los lados como los ángulos. Ya sea en problemas geométricos, ingenierías o situaciones de la vida cotidiana, el conocimiento sobre triángulos rectángulos es esencial.
Aplicación del teorema de Pitágoras para encontrar lados desconocidos
El teorema de Pitágoras es una herramienta fundamental en la geometría, especialmente cuando se trata de resolver triángulos rectángulos. Este teorema establece que en un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa (el lado opuesto al ángulo recto) es igual a la suma de los cuadrados de las longitudes de los otros dos lados, conocidos como los catetos.
La fórmula se puede representar de la siguiente manera:
c² = a² + b²
donde:
- c = longitud de la hipotenusa
- a = longitud de un cateto
- b = longitud del otro cateto
Ejemplos prácticos
Para ilustrar cómo aplicar este teorema, consideremos un triángulo rectángulo donde uno de los catetos mide 3 cm y el otro cateto mide 4 cm. Para encontrar la longitud de la hipotenusa, simplemente aplicamos la fórmula:
c² = 3² + 4²
c² = 9 + 16
c² = 25
Por lo tanto, c = 5 cm.
Uso en situaciones del mundo real
El teorema de Pitágoras no solo se aplica en situaciones académicas, sino también en diversas aplicaciones prácticas, como:
- Construcción: Para calcular la longitud de una viga que forma un triángulo rectángulo con el suelo y una pared.
- Navegación: Para determinar la distancia más corta entre dos puntos en un mapa.
- Diseño gráfico: Para crear proporciones y perspectivas correctas en objetos tridimensionales.
Tabla de ejemplos
| Cateto A (cm) | Cateto B (cm) | Hipotenusa (cm) |
|---|---|---|
| 3 | 4 | 5 |
| 5 | 12 | 13 |
| 8 | 15 | 17 |
Como se puede observar en la tabla anterior, hay tríos de números conocidos como tripletas pitagóricas que siempre satisfacen la relación del teorema de Pitágoras. Estas tripletas son especialmente útiles para resolver problemas sin necesidad de calcular raíces cuadradas.
La aplicación del teorema de Pitágoras para encontrar lados desconocidos en un triángulo rectángulo es una habilidad esencial y práctica en muchos campos. No solo facilita la resolución de problemas matemáticos, sino que también se traduce en usos cotidianos y profesionales. ¡No subestimes la simplicidad y la elegancia de esta poderosa herramienta!
Métodos para calcular ángulos utilizando razones trigonométricas
Calcular ángulos en triángulos rectángulos es una de las aplicaciones más comunes de la trigonometría. Para ello, utilizamos las razones trigonométricas, que son relaciones entre los lados de un triángulo rectángulo. Las tres razones más utilizadas son:
- Sen (seno)
- Cos (coseno)
- Tan (tangente)
Definiciones de las razones trigonométricas
A continuación, se presentan las definiciones de cada una de las razones trigonométricas en relación con un ángulo θ en un triángulo rectángulo:
- Seno (sen θ): Es la razón entre el cateto opuesto y la hipotenusa.
- Coseno (cos θ): Es la razón entre el cateto adyacente y la hipotenusa.
- Tangente (tan θ): Es la razón entre el cateto opuesto y el cateto adyacente, y se puede expresar como:
- tan θ = sen θ / cos θ
Cálculo de ángulos
Para calcular un ángulo utilizando las razones trigonométricas, se pueden aplicar las funciones inversas:
- Para el seno: θ = sen-1(opuesto/hypotenusa)
- Para el coseno: θ = cos-1(adyacente/hypotenusa)
- Para la tangente: θ = tan-1(opuesto/adyacente)
Ejemplo Práctico
Consideremos un triángulo rectángulo donde el cateto opuesto mide 4 cm y la hipotenusa mide 5 cm. Para encontrar el ángulo θ opuesto al cateto, utilizamos la razón del seno:
sen θ = cateto opuesto / hipotenusa
sen θ = 4 / 5
Ahora aplicamos la función inversa:
θ = sen-1(4/5)
Usando una calculadora, encontramos que θ ≈ 53.13°. Este tipo de cálculo es fundamental en diversas áreas, como la arquitectura y la ingeniería.
Tabla de razones trigonométricas
A continuación se presenta una tabla con ejemplos de valores comunes:
| Ángulo (°) | Sen(θ) | Cos(θ) | Tan(θ) |
|---|---|---|---|
| 0 | 0 | 1 | 0 |
| 30 | 0.5 | 0.866 | 0.577 |
| 45 | 0.707 | 0.707 | 1 |
| 60 | 0.866 | 0.5 | 1.732 |
| 90 | 1 | 0 | Indeterminado |
Estos valores son muy útiles para resolver rápidamente problemas en los que se necesite calcular los ángulos de un triángulo rectángulo.
Preguntas frecuentes
¿Qué es un triángulo rectángulo?
Un triángulo rectángulo es aquel que tiene un ángulo de 90 grados, y sus lados se llaman catetos (los que forman el ángulo recto) y la hipotenusa (el lado opuesto al ángulo recto).
¿Cómo se relacionan los catetos y la hipotenusa?
La relación entre los catetos y la hipotenusa se establece a través del teorema de Pitágoras: a² + b² = c², donde c es la hipotenusa y a y b son los catetos.
¿Qué herramientas se pueden usar para resolver triángulos rectángulos?
Se pueden usar herramientas como el teorema de Pitágoras, funciones trigonométricas (seno, coseno, tangente) y fórmulas de área y perímetro.
¿Cuándo se usa el teorema de Pitágoras?
Se utiliza el teorema de Pitágoras para calcular un lado desconocido de un triángulo rectángulo cuando se conocen los otros dos lados.
¿Qué son las funciones trigonométricas?
Las funciones trigonométricas relacionan los ángulos de un triángulo con las longitudes de sus lados y son fundamentales para resolver triángulos rectángulos.
Puntos clave sobre triángulos rectángulos
- Un triángulo rectángulo tiene un ángulo de 90 grados.
- Los dos lados que forman el ángulo recto son los catetos.
- El lado opuesto al ángulo recto se llama hipotenusa.
- Teorema de Pitágoras: a² + b² = c².
- Funciones trigonométricas: seno (sin), coseno (cos), tangente (tan).
- Área de un triángulo rectángulo: A = (base x altura) / 2.
- Perímetro: P = a + b + c.
- Los catetos son perpendiculares entre sí.
- La hipotenusa es siempre el lado más largo.
- Los triángulos rectángulos se pueden resolver usando ángulos y longitudes.
¡Dejanos tus comentarios sobre este tema y no olvides revisar otros artículos en nuestra web que también puedan interesarte!