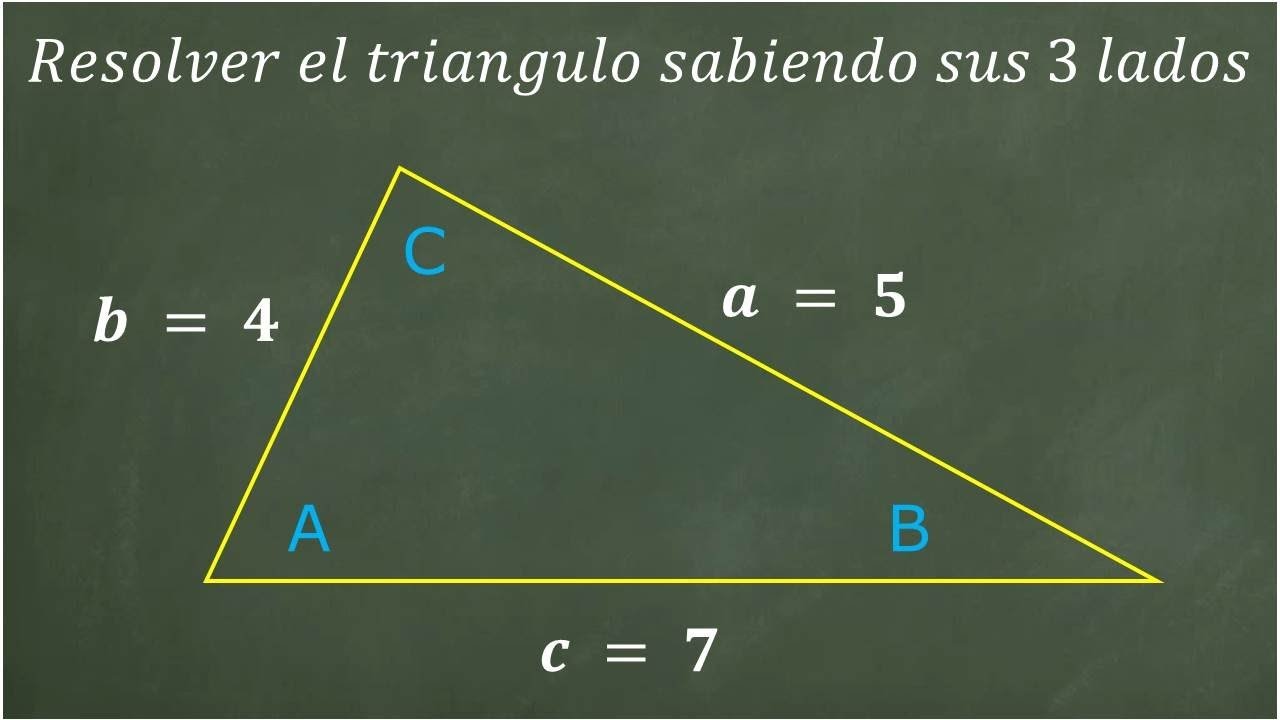
Cómo Calcular Los ángulos Internos De Un Triángulo Dados Sus Lados ✅

Usá la Ley de Cosenos: (cos(C) = frac{a^2 + b^2 – c^2}{2ab}), y luego aplicá arcoseno para obtener los ángulos. ✅

Para calcular los ángulos internos de un triángulo dados sus lados, se puede utilizar la ley de cosenos. Esta ley establece que, si conocemos las longitudes de los tres lados de un triángulo, podemos hallar cada uno de sus ángulos. La fórmula es la siguiente:

Fórmula de la Ley de Cosenos

Si tenemos un triángulo con lados a, b, y c y los ángulos opuestos a esos lados son A, B, y C, respectivamente, las relaciones son:

A: cos(A) = (b² + c² - a²) / (2bc)
B: cos(B) = (a² + c² - b²) / (2ac)
C: cos(C) = (a² + b² - c²) / (2ab)

Ejemplo Práctico

Supongamos que tenemos un triángulo con lados a = 5, b = 6, y c = 7. Para calcular el ángulo A, aplicaríamos la ley de cosenos de la siguiente manera:

A = cos^-1( (b² + c² - a²) / (2bc) )

Reemplazando los valores:

A = cos^-1( (6² + 7² - 5²) / (2 * 6 * 7) )

Calculando, nos da:

A ≈ 44.42°

Recomendaciones

Es importante recordar que la suma de los ángulos internos de un triángulo siempre es 180 grados. Por lo tanto, si ya conoces uno o dos ángulos, puedes calcular el tercero restando la suma de los conocidos de 180°.

En el caso de utilizar un software o calculadora gráfica, estas herramientas suelen tener funciones que te permiten calcular los ángulos directamente a partir de las longitudes de los lados, haciendo el proceso más ágil y sencillo.

Resumen de Pasos

Identifica las longitudes de los tres lados.
Aplica la ley de cosenos para cada ángulo.
Verifica que la suma de los ángulos sea 180°.

Fórmula del coseno para encontrar ángulos a partir de lados

La fórmula del coseno es una herramienta fundamental en la geometría que permite calcular los ángulos internos de un triángulo cuando se conocen las longitudes de sus lados. Esta fórmula se expresa de la siguiente manera:

Cómo puedo evitar que llueva en un evento al aire libre

c² = a² + b² – 2ab * cos(C)

Donde:

a y b son las longitudes de los lados adyacentes al ángulo C.
c es la longitud del lado opuesto al ángulo C.

Ejemplo Práctico

Supongamos que tenemos un triángulo con lados de longitud a = 5, b = 7 y c = 10. Queremos encontrar el ángulo C.

Aplicamos la fórmula:

10² = 5² + 7² – 2 * 5 * 7 * cos(C)

Resolviendo los cuadrados, obtenemos:

100 = 25 + 49 – 70 * cos(C)

Simplificando:

100 = 74 – 70 * cos(C)

70 * cos(C) = 74 – 100

70 * cos(C) = -26

cos(C) = -26 / 70

cos(C) ≈ -0.3714

Ahora, utilizando la calculadora de cosenos o la función inversa, calculamos el ángulo C:

C ≈ 108.2°

Tabla de Comparación de Ángulos

Lado a	Lado b	Lado c	Ángulo C (°)
5	7	10	108.2
6	8	10	75.5
7	9	12	64.6

Consejos Prácticos

Verificar la validez de los lados antes de calcular los ángulos: la suma de las longitudes de dos lados siempre debe ser mayor que la longitud del tercer lado.
Utilizar siempre una calculadora científica para obtener resultados precisos en el cálculo de las funciones trigonométricas.
Practicar con diferentes conjuntos de lados para familiarizarse con la aplicación de la fórmula del coseno.

La fórmula del coseno no solo es útil para triángulos, sino que también se utiliza extensamente en aplicaciones de navegación, ingeniería, y arquitectura, donde es crucial entender las relaciones entre los lados y los ángulos. No dudes en profundizar en su uso para mejorar tu comprensión de la geometría.

Ejercicios prácticos para calcular ángulos interiores de triángulos

Para calcular los ángulos interiores de un triángulo dados sus lados, existen varios métodos prácticos que podemos aplicar. A continuación, te presentamos una serie de ejercicios que te ayudarán a dominar este concepto.

Cuánto cuesta la entrada al Museo de Boca Juniors

Método de la Ley de Cosenos

La Ley de Cosenos es una herramienta poderosa que nos permite encontrar los ángulos de un triángulo cuando conocemos la longitud de sus lados. La fórmula es la siguiente:

c² = a² + b² – 2ab * cos(C)

Donde:

a, b, c son los lados del triángulo.
C es el ángulo opuesto al lado c.

Vamos a ver un ejemplo concreto:

Ejemplo 1

Supongamos que tenemos un triángulo con lados de longitud a = 5, b = 7 y c = 10.

Aplicamos la fórmula para encontrar el ángulo C:
10² = 5² + 7² – 2 * 5 * 7 * cos(C)
Desarrollando la ecuación:

100 = 25 + 49 – 70 * cos(C)
100 = 74 – 70 * cos(C)
26 = -70 * cos(C)
cos(C) = -26/70
C = cos⁻¹(-0.3714) ≈ 111.8°

Por lo tanto, hemos calculado el ángulo C del triángulo. Para calcular los otros ángulos (A y B) podemos usar el mismo método o recurrir a la Ley de Sines.

Método de la Ley de Sines

La Ley de Sines establece que:

sin(A)/a = sin(B)/b = sin(C)/c

Esta ley es útil cuando conocemos al menos un ángulo y sus lados. Sigamos con nuestro ejemplo anterior, ahora supongamos que queremos calcular el ángulo A.

Ejemplo 2

Con los valores obtenidos:

Utilizamos la Ley de Sines.
sin(A)/5 = sin(111.8°)/10

Despejamos A:
sin(A) = 5 * sin(111.8°)/10
Calculamos:

sin(111.8°) ≈ 0.9272
sin(A) = 5 * 0.9272 / 10 ≈ 0.4636
A = sin⁻¹(0.4636) ≈ 27.6°

Finalmente, podemos encontrar el ángulo B usando la suma de ángulos interiores en un triángulo, que siempre es 180°:

B = 180° – A – C = 180° – 27.6° – 111.8° ≈ 40.6°

Tabla de ejemplos

Lado A	Lado B	Lado C	Ángulo A	Ángulo B	Ángulo C
5	7	10	27.6°	40.6°	111.8°
6	8	10	36.9°	53.1°	90.0°

Practicar diferentes ejercicios te ayudará a familiarizarte con estos métodos. Recuerda siempre verificar tus cálculos y usar herramientas como calculadoras científicas para asegurarte de obtener resultados precisos.

Cómo llegar a Pehuen Co en colectivo desde diferentes ciudades