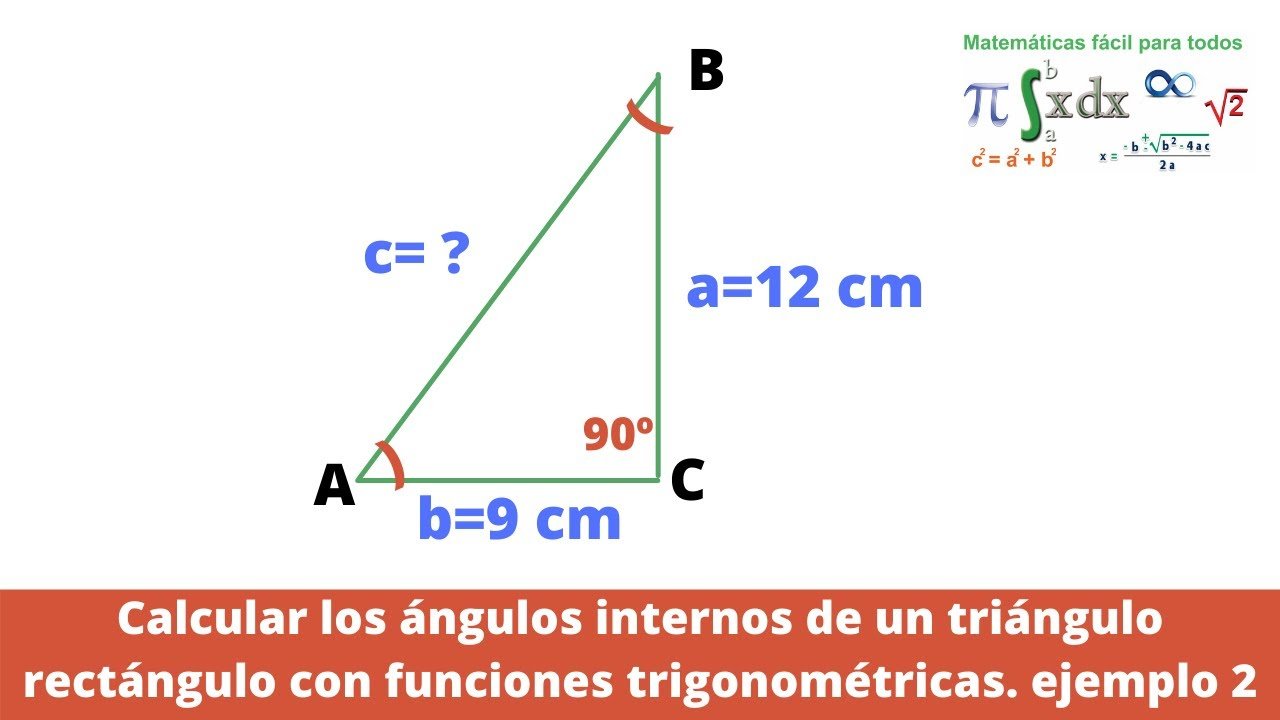
Cómo usar una calculadora para encontrar los ángulos de un triángulo rectángulo
Usá funciones trigonométricas: «sin», «cos», «tan». Ingresá lados y obtené ángulos con inverso «sin-1», «cos-1», «tan-1». ¡Simple y eficaz! ✅
Para encontrar los ángulos de un triángulo rectángulo usando una calculadora, es fundamental que comprendas las relaciones trigonométricas básicas. En un triángulo rectángulo, uno de los ángulos es siempre de 90 grados. Los otros dos ángulos son complementarios, lo que significa que su suma es igual a 90 grados. Por lo tanto, si conoces uno de los ángulos, puedes fácilmente encontrar el otro ángulo restando el ángulo conocido de 90 grados.
Para calcular los ángulos restantes utilizando una calculadora científica, puedes emplear la función de arcoseno, arcocoseno o arcotangente. Por ejemplo, si conoces las longitudes de los lados adyacente y opuesto, puedes usar la función tan (tangente) para encontrar uno de los ángulos:
- tan(ángulo) = lado opuesto / lado adyacente
- ángulo = arctan(lado opuesto / lado adyacente)
Aquí tienes un ejemplo práctico: Supón que tienes un triángulo rectángulo con un lado opuesto de 3 cm y un lado adyacente de 4 cm. Para encontrar el ángulo, deberías calcular:
ángulo = arctan(3 / 4)
Esto te dará el valor del ángulo en radianes o grados, dependiendo de la configuración de tu calculadora.
Además, si conoces la hipotenusa y uno de los catetos, puedes usar el arcoseno o arcocoseno para encontrar los ángulos:
- sen(ángulo) = lado opuesto / hipotenusa
- ángulo = arcsin(lado opuesto / hipotenusa)
- cos(ángulo) = lado adyacente / hipotenusa
- ángulo = arccos(lado adyacente / hipotenusa)
Es importante recordar que, en muchos casos, las calculadoras te mostrarán el resultado en radianes. Si necesitas el resultado en grados, busca el botón de conversión en tu calculadora o cambia la configuración de modo. Con estos simples pasos, podrás utilizar la calculadora para determinar los ángulos de cualquier triángulo rectángulo con facilidad.
Paso a paso: Calcular ángulos usando funciones trigonométricas en calculadoras
Utilizar una calculadora para encontrar ángulos en un triángulo rectángulo es bastante sencillo si comprendemos las funciones trigonométricas básicas. A continuación, se presenta un paso a paso que te ayudará a dominar esta técnica.
1. Identifica los lados del triángulo
Primero, es fundamental que identifiques los lados del triángulo rectángulo. Recuerda que en este tipo de triángulo, uno de los ángulos es de 90 grados. Los otros dos ángulos son los que nos interesan calcular. Los lados se denominan:
- Cateto opuesto: el lado opuesto al ángulo que deseas calcular.
- Cateto adyacente: el lado que está junto al ángulo que deseas calcular.
- Hipotenusa: el lado más largo, opuesto al ángulo recto.
2. Selecciona la función trigonométrica adecuada
Una vez identificados los lados, el siguiente paso es elegir la función trigonométrica que se ajusta a la situación. Existen tres funciones principales:
- Seno (sin): se utiliza para calcular el ángulo cuando se conocen el cateto opuesto y la hipotenusa. La fórmula es: sin(θ) = cateto opuesto / hipotenusa.
- Coseno (cos): se utiliza para calcular el ángulo cuando se conocen el cateto adyacente y la hipotenusa. La fórmula es: cos(θ) = cateto adyacente / hipotenusa.
- Tangente (tan): se utiliza para calcular el ángulo cuando se conocen el cateto opuesto y el cateto adyacente. La fórmula es: tan(θ) = cateto opuesto / cateto adyacente.
3. Usa la calculadora
Ahora que tienes la información necesaria, sigue estos pasos para calcular el ángulo:
- Ingresa los valores de los lados en la función correspondiente.
- Realiza la operación matemática para encontrar el valor de la función.
- Utiliza la función inversa de la trigonometría para encontrar el ángulo. Por ejemplo, si usaste el seno, deberás usar arcoseno (sin-1) para calcular el ángulo.
Ejemplo práctico
Supongamos que tienes un triángulo rectángulo donde el cateto opuesto mide 3 cm y la hipotenusa mide 5 cm. Para encontrar el ángulo:
- Usa la función seno: sin(θ) = 3 / 5.
- Calcula el valor: sin(θ) = 0.6.
- Ahora, usa la función inversa: θ = sin-1(0.6).
- La calculadora te dará aproximadamente 36.87 grados como resultado.
Consejos prácticos
Para facilitar el proceso, ten en cuenta los siguientes consejos:
- Asegúrate de que la calculadora esté en el modo correcto (grados o radianes) dependiendo de cómo quieras expresar el ángulo.
- Practica con diferentes triángulos para familiarizarte con el uso de las funciones trigonométricas.
- Recuerda que la precisión en la medición de los lados es fundamental para obtener un resultado exacto.
Tabla de funciones trigonométricas
| Función | Ratio |
|---|---|
| Seno (sin) | Cateto opuesto / Hipotenusa |
| Coseno (cos) | Cateto adyacente / Hipotenusa |
| Tangente (tan) | Cateto opuesto / Cateto adyacente |
Errores comunes al encontrar ángulos de un triángulo rectángulo con calculadoras
Al utilizar una calculadora para determinar los ángulos de un triángulo rectángulo, es crucial evitar ciertos errores comunes que pueden llevar a resultados incorrectos. A continuación, se presentan algunos de estos errores y cómo prevenirlos.
1. No cambiar la configuración de la calculadora
Una de las principales causas de confusión al trabajar con ángulos es la configuración de la calculadora. Las calculadoras pueden estar configuradas en modo grados o radianos. Si estás trabajando con medidas en grados, asegúrate de que la calculadora esté en ese modo.
- Ejemplo: Si ingresas el valor de un ángulo en radianes, como 1.57, y la calculadora está en modo grados, obtendrás un resultado erróneo.
2. Olvidar aplicar la fórmula correcta
Los errores de fórmula son bastante comunes. Al calcular ángulos, es importante recordar que existen diferentes relaciones trigonométricas que se pueden utilizar, como sen, cos y tan. Asegúrate de aplicar la fórmula adecuada según la información que tengas.
- Utiliza la fórmula del seno: sen(α) = opuesto / hipotenusa
- Utiliza la fórmula del coseno: cos(α) = adyacente / hipotenusa
- Utiliza la fórmula de la tangente: tan(α) = opuesto / adyacente
3. Desestimar la importancia de los triángulos congruentes
A veces, los cálculos pueden ser confusos debido a la presencia de triángulos congruentes. Es importante recordar que si un triángulo es congruente a otro, sus ángulos son iguales. Esto puede llevar a errores si no se toman en cuenta.
4. No verificar los resultados
Siempre es recomendable verificar los resultados. Después de encontrar un ángulo, puedes utilizar la suma de los ángulos en un triángulo rectángulo, que siempre debe ser 180 grados, para comprobar tu respuesta. Si los ángulos no suman 180 grados, hay un error en los cálculos.
Al usar una calculadora para encontrar los ángulos de un triángulo rectángulo, es fundamental prestar atención a la configuración de la herramienta, aplicar las fórmulas adecuadas, considerar la congruencia de los triángulos y siempre verificar los resultados. Cuidar estos detalles te permitirá obtener respuestas más precisas y confiables.
Preguntas frecuentes
¿Qué es un triángulo rectángulo?
Es un triángulo que tiene un ángulo de 90 grados.
¿Cómo se encuentran los ángulos con una calculadora?
Utilizando funciones trigonométricas como seno, coseno o tangente.
¿Qué datos necesito para calcular los ángulos?
Conocer al menos un ángulo agudo y un lado, o dos lados del triángulo.
¿Puedo usar cualquier calculadora?
No, necesitas una calculadora científica que tenga funciones trigonométricas.
¿Es necesario conocer la regla de los senos o cosenos?
Es recomendable, ya que facilita el cálculo de los ángulos en triángulos no rectángulos.
¿Cuáles son las propiedades de los ángulos en un triángulo?
La suma de los ángulos siempre es 180 grados y en un triángulo rectángulo, uno de ellos es 90 grados.
Puntos clave para calcular ángulos en un triángulo rectángulo
- Identificar el triángulo rectángulo.
- Conocer un ángulo agudo y un lado, o dos lados.
- Utilizar funciones trigonométricas: seno, coseno y tangente.
- Aplicar la fórmula correspondiente:
- Seno: opuesto/hipotenusa
- Coseno: adyacente/hipotenusa
- Tangente: opuesto/adyacente
- Usar una calculadora científica para obtener resultados precisos.
- Verificar los resultados con la suma de los ángulos.
¡Dejanos tu comentario!
Si tienes más preguntas o te gustaría compartir tu experiencia, ¡déjanos tu comentario! También te invitamos a revisar otros artículos de nuestra web que pueden interesarte.