Cuánto es x al cuadrado en matemáticas y cómo se calcula
Para calcular x al cuadrado, simplemente multiplicás x por sí mismo: x² = x * x. ¡Es un concepto fundamental en álgebra! ✅
En matemáticas, x al cuadrado se refiere a la operación de elevar una variable o número x a la potencia de 2. Esto se expresa como x² y se calcula multiplicando x por sí mismo. Por ejemplo, si x es 3, entonces x² es igual a 3 * 3, lo que da como resultado 9.
El cálculo de x al cuadrado es una operación fundamental en álgebra y tiene aplicaciones en diversas áreas de las matemáticas, desde la resolución de ecuaciones hasta el análisis de gráficos. Exploraremos más a fondo el concepto de elevar un número al cuadrado, ejemplos prácticos y algunos consejos para facilitar el entendimiento de esta operación.
¿Qué significa elevar al cuadrado?
Elevar un número o variable al cuadrado es uno de los tipos más comunes de operaciones exponentes. La notación x² implica que el número x se multiplica por sí mismo. Es importante tener en cuenta que:
- Si x es positivo, x² también será positivo.
- Si x es cero, entonces x² será cero.
- Si x es negativo, x² se convertirá en positivo, ya que el producto de dos números negativos es positivo.
Ejemplos de cálculo de x²
A continuación, se presentan algunos ejemplos prácticos de cómo calcular x al cuadrado:
- Si x = 2, entonces x² = 2 * 2 = 4.
- Si x = -5, entonces x² = -5 * -5 = 25.
- Si x = 0, entonces x² = 0 * 0 = 0.
Propiedades del cuadrado de un número
Al elevar un número al cuadrado, existen varias propiedades que son útiles:
- (a + b)² = a² + 2ab + b²: Esta es la fórmula del cuadrado de una suma.
- (a – b)² = a² – 2ab + b²: Esta es la fórmula del cuadrado de una diferencia.
- (-x)² = x²: Elevar un número negativo al cuadrado da el mismo resultado que elevar su equivalente positivo.
Aplicaciones de x² en el mundo real
El concepto de elevar al cuadrado tiene múltiples aplicaciones prácticas. Algunas de ellas son:
- En física, para calcular áreas de superficies.
- En estadística, para determinar la varianza.
- En arquitectura y diseño, para el cálculo de volúmenes y áreas de estructuras.
Conceptos básicos de la potencia al cuadrado en matemáticas
La potencia al cuadrado es una operación matemática fundamental que se utiliza frecuentemente en diversas áreas, desde la geometría hasta la estadística. Se refiere al resultado de multiplicar un número por sí mismo. Por ejemplo, si tenemos un número x, su cuadrado se expresa como x² y se calcula de la siguiente manera:
- x² = x × x
Ejemplos Prácticos
Veamos algunos ejemplos concretos para entender mejor esta operación:
- Si x = 3, entonces 3² = 3 × 3 = 9.
- Si x = 5, entonces 5² = 5 × 5 = 25.
- Si x = 10, entonces 10² = 10 × 10 = 100.
Además, el cuadrado de un número puede tener aplicaciones prácticas en situaciones cotidianas. Por ejemplo, si deseamos calcular el área de un cuadrado, podemos usar la fórmula:
- Área = lado²
Características de la potencia al cuadrado
Algunas propiedades importantes de la potencia al cuadrado son:
- El resultado siempre es un número no negativo (ya que multiplicar dos números negativos o positivos da como resultado un número positivo).
- El cuadrado de cero es cero: 0² = 0.
- La regla del signo: el cuadrado de un número negativo también es positivo, por ejemplo, (-4)² = 16.
Aplicaciones en el mundo real
La operación de elevar al cuadrado se utiliza en diversas disciplinas, tales como:
- Física: Para calcular la energía cinética, donde se utiliza la fórmula KE = 1/2 mv².
- Arquitectura: Para determinar áreas y volúmenes en la construcción.
- Estadística: En el cálculo de la varianza y el desvío estándar.
Resumen de la operación
Para resumir, la potencia al cuadrado es una herramienta matemática esencial que permite realizar cálculos importantes en diferentes áreas. Conocer cómo calcular x² y comprender sus aplicaciones prácticas es fundamental para el desarrollo de habilidades matemáticas sólidas.
Ejemplos prácticos de cálculo de x al cuadrado en diferentes contextos
Calcular x al cuadrado es una de las operaciones más básicas pero también esenciales en matemáticas. A continuación, exploraremos algunos ejemplos concretos y casos de uso que ilustran cómo se aplica esta operación en diferentes contextos.
1. Contexto geométrico
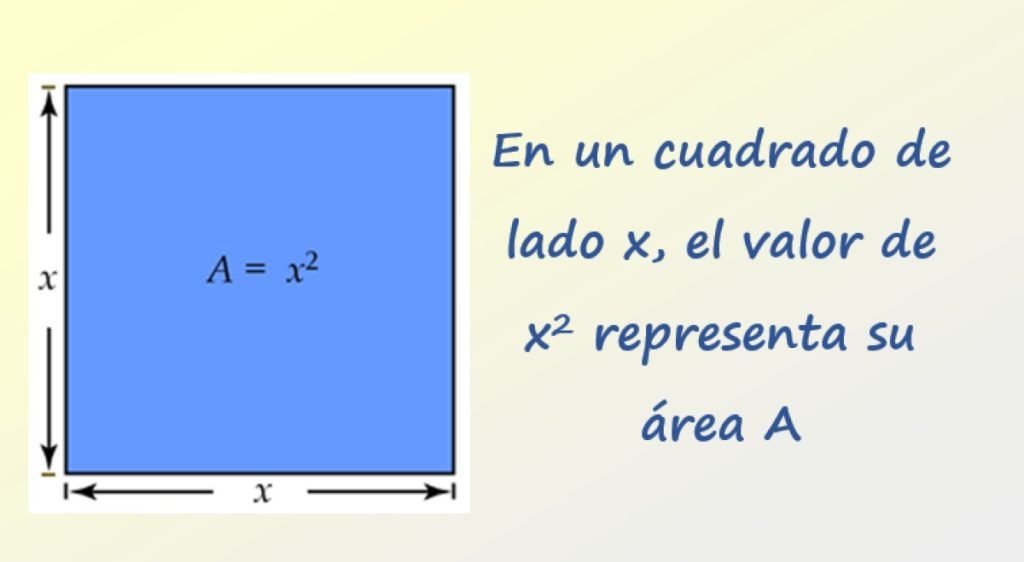
En geometría, el cálculo de x al cuadrado es fundamental para determinar el área de un cuadrado. La fórmula para calcular el área (A) de un cuadrado es:
A = x², donde x es la longitud de uno de sus lados.
- Si un cuadrado tiene un lado de 4 cm, entonces:
- A = 4² = 16 cm²
- Si un cuadrado tiene un lado de 5 cm, entonces:
- A = 5² = 25 cm²
2. Contexto financiero
En finanzas, el cálculo de x al cuadrado es útil para analizar el rendimiento de inversiones. Por ejemplo, si se invierte una cantidad x y se espera que esta inversión crezca al cuadrado, se puede calcular el rendimiento esperado. Supongamos que la inversión inicial es de $200:
Rendimiento esperado = (200)² = $40,000.
3. Contexto físico
En física, la fórmula de la energía cinética (E) de un objeto en movimiento está dada por:
E = ½ * m * v², donde m es la masa y v es la velocidad del objeto.
Si un objeto tiene una masa de 2 kg y se mueve a 3 m/s, su energía cinética sería:
- E = ½ * 2 * (3)²
- E = 3 * 9 = 27 J
4. Contexto algorítmico
En programación, calcular x al cuadrado es una operación común. Por ejemplo, en un lenguaje como Python, podríamos tener el siguiente código:
x = 5
resultado = x 2
print(resultado) # Esto imprimirá 25
Este tipo de cálculo se utiliza en diversos algoritmos y funciones matemáticas, facilitando la resolución de problemas complejos.
5. Comparativa de métodos de cálculo
A continuación, se presenta una tabla que compara diferentes métodos para calcular x al cuadrado:
| Método | Descripción | Ejemplo |
|---|---|---|
| Multiplicación | Multiplicar x por sí mismo | 3 * 3 = 9 |
| Uso de potencias | Usar la función de potencia | 2 2 = 4 |
| Calculadora | Utilizar una calculadora científica | Ingresar 4 y presionar x² |
Como hemos visto, el cálculo de x al cuadrado tiene múltiples aplicaciones prácticas en diferentes disciplinas. Estos ejemplos no solo facilitan la comprensión de la operación, sino que también muestran su relevancia en el mundo real.
Preguntas frecuentes
¿Qué significa x al cuadrado?
x al cuadrado, escrito como x², representa el número x multiplicado por sí mismo.
¿Cómo se calcula x²?
Para calcular x², simplemente multiplicás el valor de x por sí mismo.
¿Qué valor tiene x² si x=3?
Si x=3, entonces x² = 3 * 3 = 9.
¿Existen propiedades de los cuadrados?
Sí, por ejemplo, el cuadrado de un número negativo es positivo: (-x)² = x².
¿Cómo se aplica x² en la vida real?
Se utiliza en áreas como la física, la economía y la estadística, entre otras.
| Punto clave | Descripción |
|---|---|
| Definición | x² es x multiplicado por x. |
| Ejemplo básico | Para x=4, x²=16. |
| Propiedad de los cuadrados | El cuadrado de una suma se expande como (a+b)² = a² + 2ab + b². |
| Uso en geometría | El área de un cuadrado se calcula como lado². |
| Relación con funciones | La función cuadrática se representa como f(x) = ax² + bx + c. |
¡Dejanos tus comentarios! No olvides revisar otros artículos de nuestra web que pueden interesarte.